In Chapter 2 of Bayesian Methods for Hackers, there's an example of
Bayesian analysis of an A/B test using simulated data. I decided to play
around with this analysis method with real A/B landing page test data
from one of my clients.
This method uses PyMC to estimate the real conversion rate for each page
and Matplotlib to visually interpret the results.
First, I import the relevant packages:
import numpy as np
import pymc as pm
import matplotlib.pyplot as plt
My client ran a landing page test with the following results:
clicks_A = 1135
orders_A = 5
clicks_B = 1149
orders_B = 17
The observed conversion rates are 44% and 1.48% for pages A and B,
respectively, but I'd like to be confident that the true conversion rate
of page B is higher than page A.
To format this data for the analysis, I create a numpy array for each
page with 1s representing orders and 0s representing clicks without an
order:
data_A = np.r_[[0] * (clicks_A - orders_A), [1] * orders_A]
data_B = np.r_[[0] * (clicks_B - orders_B), [1] * orders_B]
Next I assign distributions to my prior beliefs of p_A and p_B, the unknown, true conversion rates. I
assume, for simplicity, that the distributions are uniform (i.e. I have
no prior knowledge of what p_A and 'p_B' are).
[Note: the rest of the code in blog post is taken from [the book].
p_A = pm.Uniform('p_A', lower=0, upper=1)
p_B = pm.Uniform('p_B', lower=0, upper=1)
Since I want to estimate the difference in true conversion rates, I need
to define a variable delta, which equals p_B - p_A. Since, if I know
both p_A and p_B, I can calculate delta, it's a deterministic
variable. In PyMC, deterministic variables are created using a function
with a pymc.deterministic wrapper:
@pm.deterministic
def delta(p_A=p_A, p_B=p_B):
return p_B - p_A
Next I add the observed data to PyMC variables and run an inference
algorithm (I don't understand what this code is actually doing yet - an
explanation is coming up in Chapter 3):
obs_A = pm.Bernoulli("obs_A",
p_A, value = data_A, observed = True)
obs_B = pm.Bernoulli("obs_B", p_B, value = data_B, observed = True)
mcmc = pm.MCMC([p_A, p_B, delta, obs_A, obs_B])
mcmc.sample(20000, 1000)
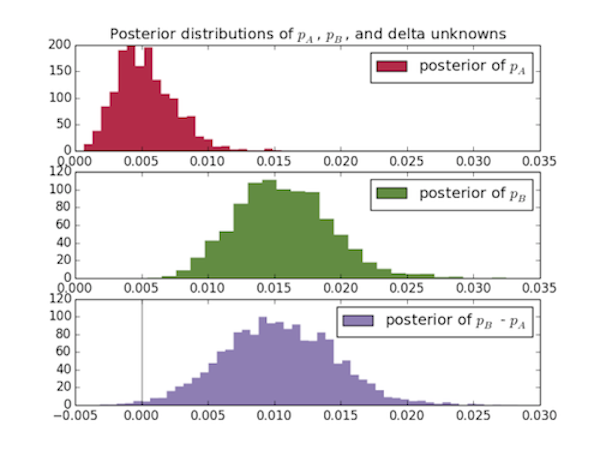
Then I plot the posterior distributions for the three unknowns:
p_A_samples = mcmc.trace("p_A")[:]
p_B_samples = mcmc.trace("p_B")[:]
delta_samples = mcmc.trace("delta")[:]
ax = plt.subplot(311)
plt.xlim(0, .035)
plt.hist(p_A_samples, histtype='stepfilled', bins=25, alpha=0.85,
label="posterior of $p_A$", color="#A60628", normed=True,
edgecolor= "none")
plt.legend(loc="upper right")
plt.title("Posterior distributions of $p_A$, $p_B$, and delta
unknowns")
ax = plt.subplot(312)
plt.xlim(0, .035)
plt.hist(p_B_samples, histtype='stepfilled', bins=25, alpha=0.85,
label="posterior of $p_B$", color="#467821", normed=True,
edgecolor = "none")
plt.legend(loc="upper right")
ax = plt.subplot(313)
plt.ylim(0,120)
plt.hist(delta_samples, histtype='stepfilled', bins=50, alpha=0.85,
label="posterior of $p_B$ - $p_A$", color="#7A68A6",normed=True,
edgecolor = "none")
plt.legend(loc="upper right")
plt.vlines(0, 0, 120, color="black", alpha = .5)
plt.show()
I can also compute the probability that the true conversion rate of page
A, p_A, is better than the true conversion rate of page
B, p_A:
print "Probability site A is BETTER than site B: %.3f" %
(delta_samples < 0).mean()
print "Probability site A is WORSE than site B: %.3f" %
(delta_samples > 0).mean()
This should print out:
Probability page A is BETTER than page B: 0.006
Probability page A is WORSE than page B: 0.994
It's very safe to say (as long as our data was collected properly) that
page B is better than page A, and these results come very intuitively
from looking at the graphs.
The full code can be found on my GitHub.
tags:
ab testing
matplotlib
numpy
pymc
python
There are probably no comments.